Regularization
좋은 모델은 현재 데이터를 잘 설명하고, 미래 데이터에 대해 잘 예측하는 모델이다.
- train data error 최소 (현재)
- test data error 최소 (미래)
bias는 손해를 보더라도 variance를 좋게해서 성능을 좋게함


Regularization 개념


계수 β에 패널티를 준다.
결국 계수가 0이 되어야 되며, 차수가 낮아진다.




Ridge Regression
L2-norm제약(제곱)





판별식이 < 0이므로 타원의 형태임, 따라서 MSE contour는 타원의 형태를 가짐



최소제곱의 β는 unbias 이지만, ridge의 β는 bias된다. 그러나 variance가 작아져 예측이 좋아진다.
※ closed-form solution은 문제에 대한 해답을 식으로 명확하게 제시할 수 있다는 것을 의미
Lasso regression
L1-norm제약 (절대값)







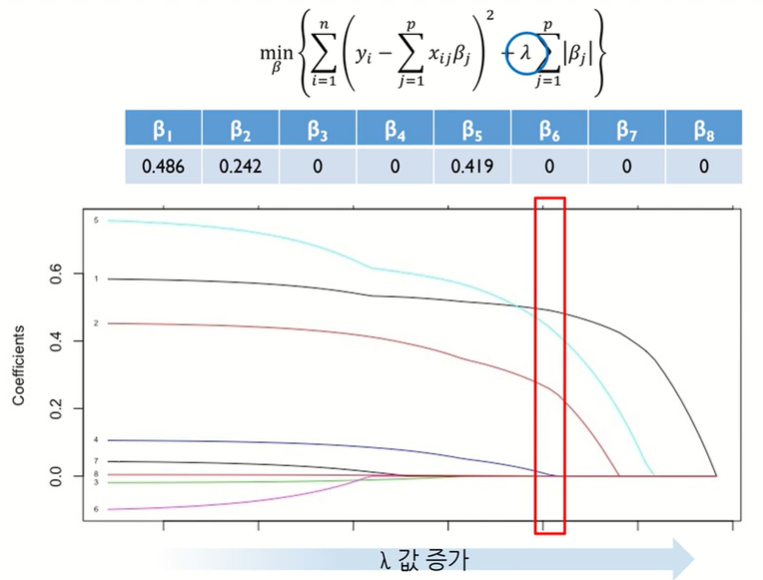
Lasso는 데이터가 바뀌어도 강건하다. (Robust)
Ridge vs. Lasso
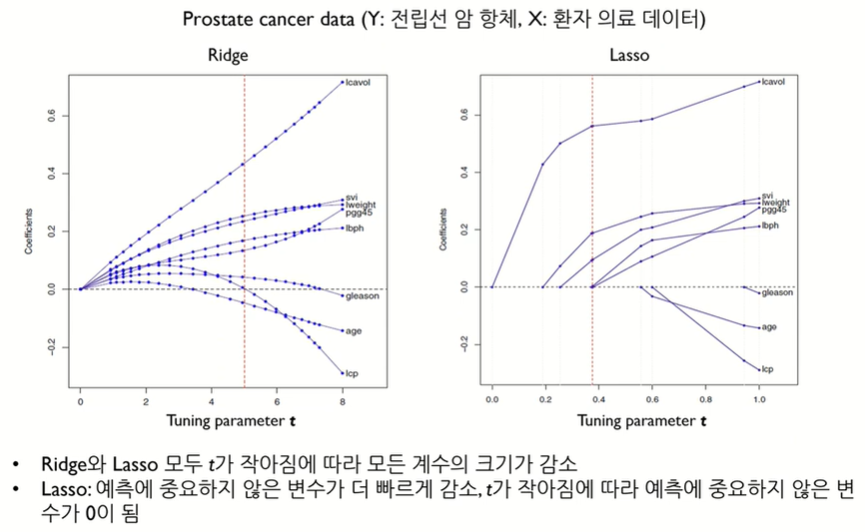
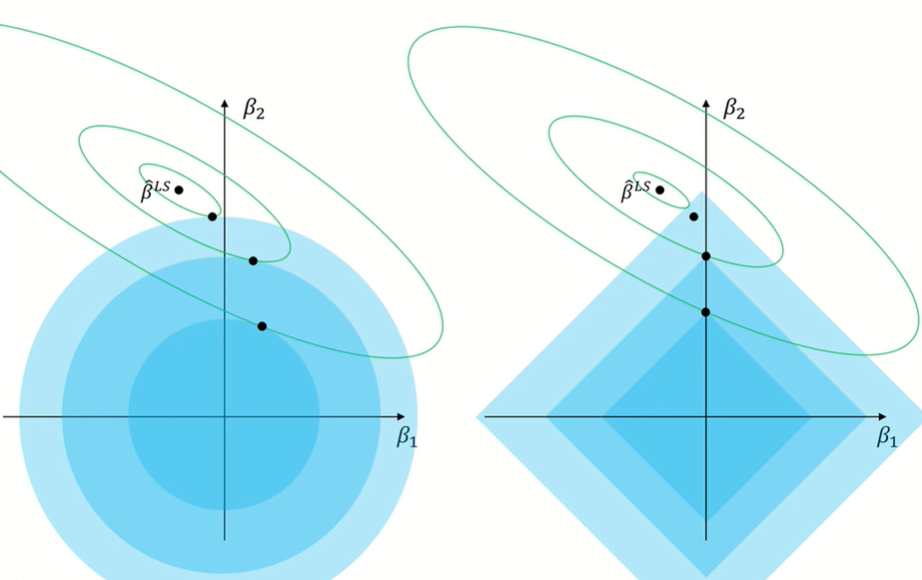
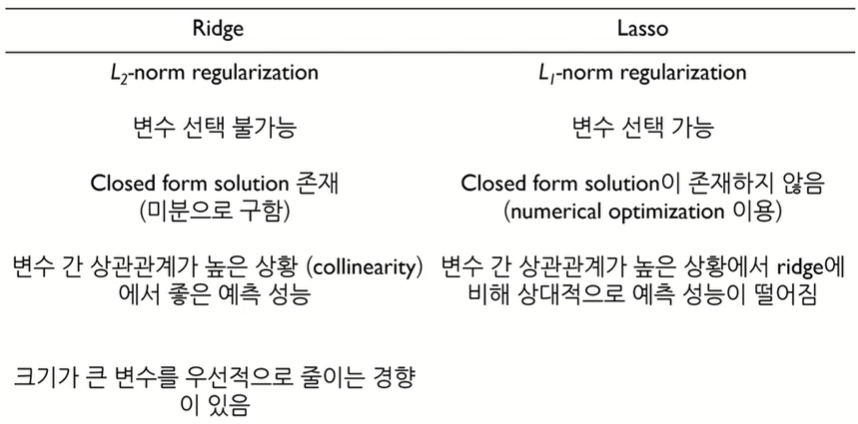
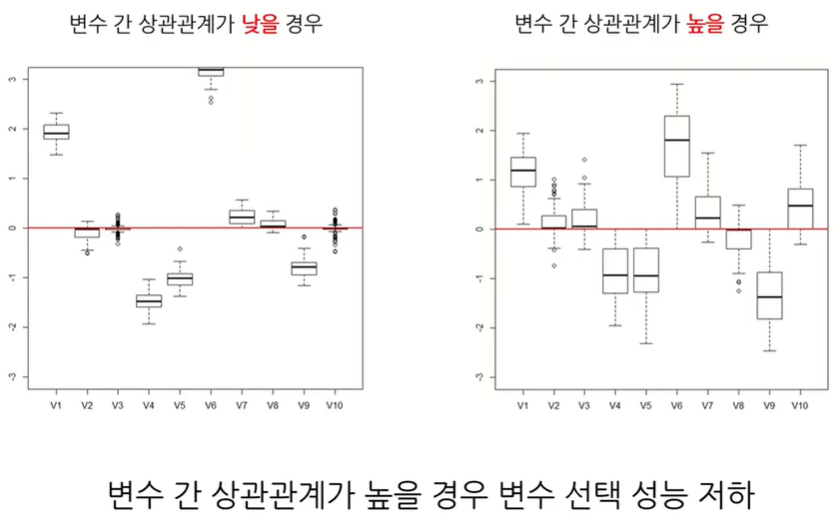
Lasso의 한계점
변수간 상관관계가 높으면 데이터가 변할때마다 예측이 흔들린다. Robust하지 않게됨
Elastic regression
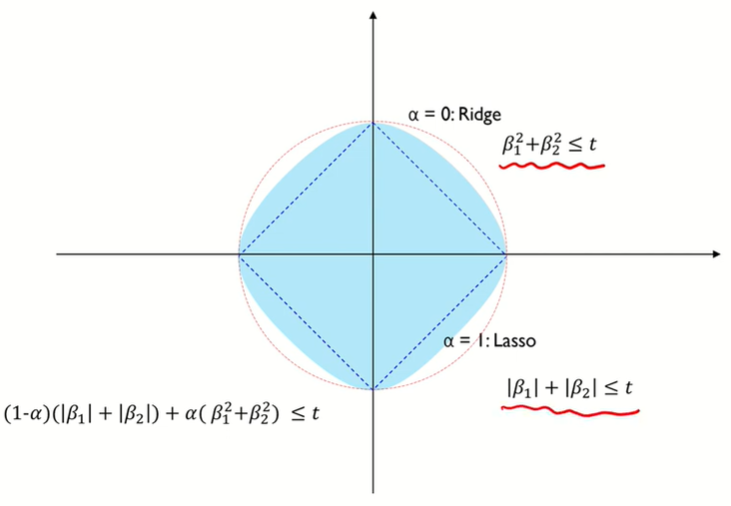
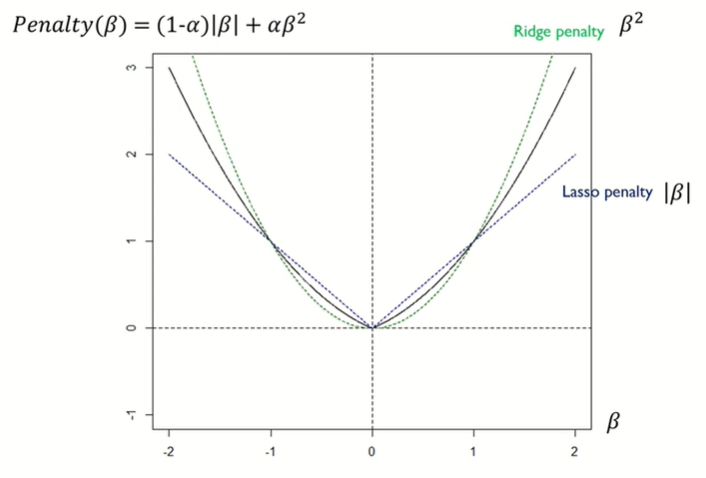
Lasso의 한계를 극복하고자 나옴


변수간 상관관계가 매우 높으면 β는 같은 값으로 보겠다는 것 (같은 패턴으로 추정 : Grouping effect)
λ2를 크게하면 β가 작아지는 효과가 있다.
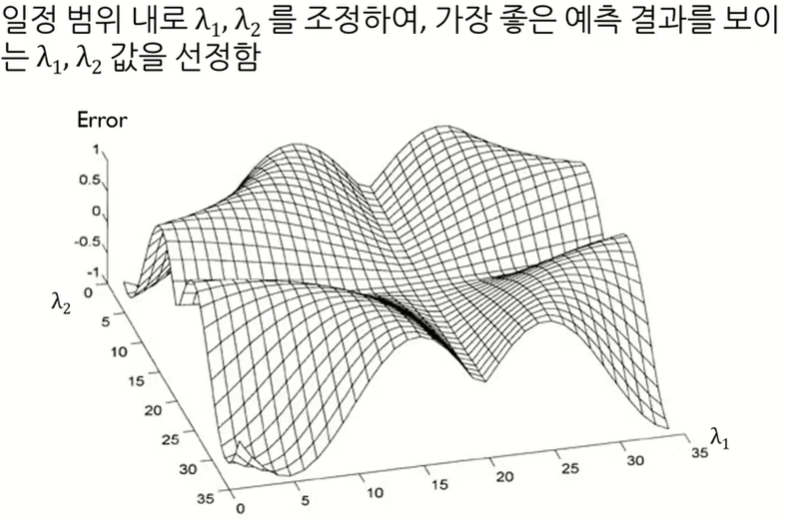
Regularization with Prior Knowledge
사전지식을 이용하여 제약을하는 정규화

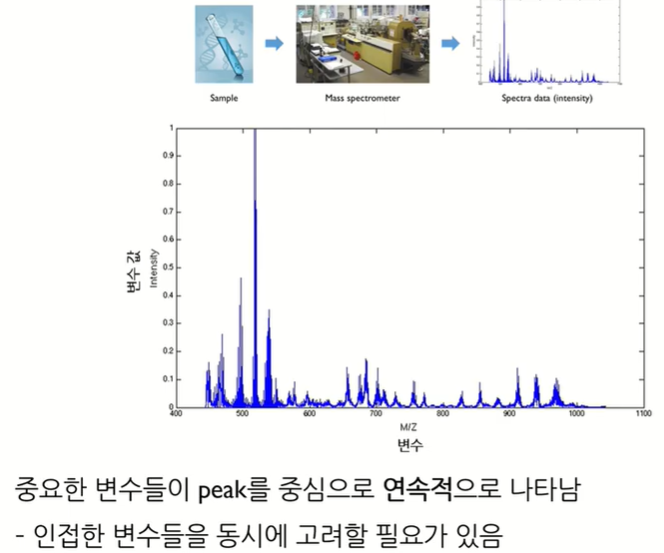
Fused Lasso
signal, profile, spectra에 사용

Group Lasso
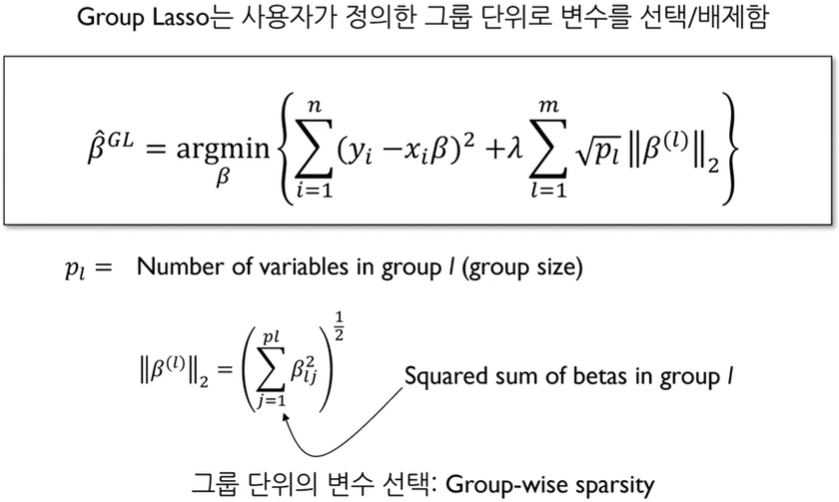
Sparse group Lasso
그룹내에서 한번 더 중요변수를 거른다. Lasso가 추가됨

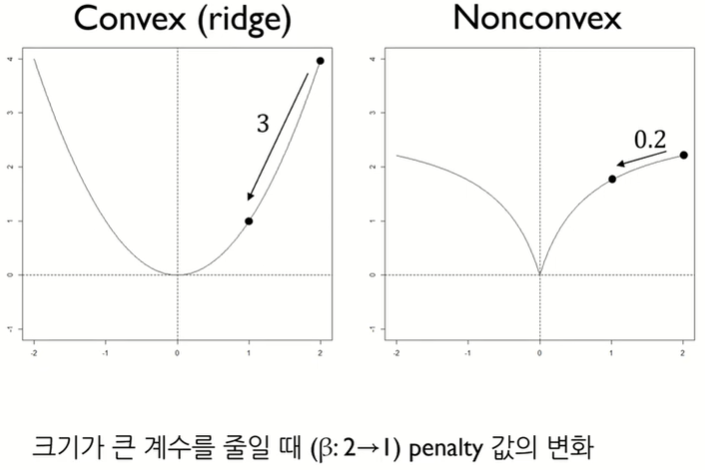
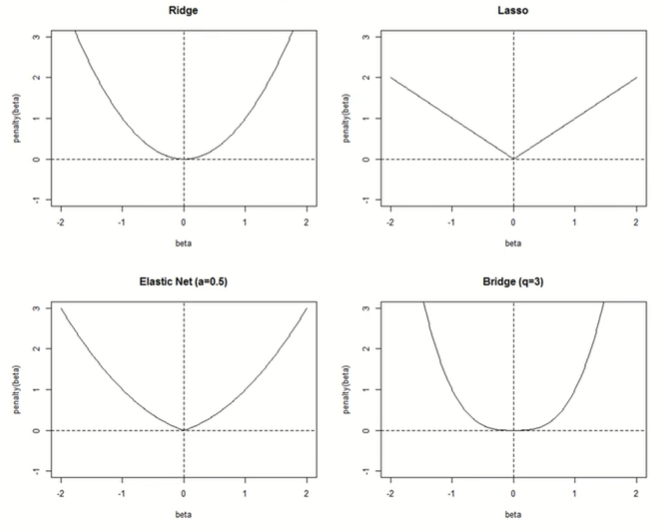
Nonconvex Penalty
앞서 배운 정규화는 convex를 가정하나, nonconvex에 대한 경우도 존재함


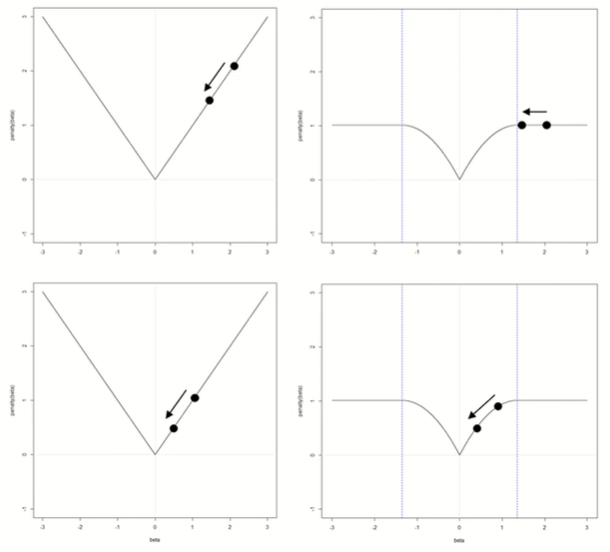

'Machine Learning' 카테고리의 다른 글
| 의사결정나무 Decision Tree (0) | 2024.04.13 |
|---|---|
| KNN (K-Nearest Neighbor, K-최근접 이웃) (0) | 2024.04.13 |
| 뉴럴네트워크모델 (0) | 2024.04.13 |
| 로지스틱회귀모델 Logistic Regression (0) | 2024.04.13 |
| 선형회귀모델 Regression (0) | 2024.04.13 |